아는만큼 Search tree

Written by hackerwins on May 10, 2019

회사 일을 하면서 자료구조를 구현할 기회는 별로 없었다. 하지만 최근에 데이터 타입 기반 동기화 플랫폼을 개발하면서 운 좋게도 일부 자료구조를 직접 구현해야만 했다. 나중에 잊어버리는 것보다는 짧은 지식이라도 적는게 나은 것 같아서 아는 만큼이라도 기록하기로 했다. 이 글은 마지막에 있는 링크들을 참고해서 정리했다.

Binary search tree

Binary search tree(이하 BST)는 Binary tree 형식의 자료 구조이다. BST에서 노드의 왼쪽 하위 트리(subtree)의 모든 노드의 Key는 현재 노드의 Key보다 작아야 하고 오른쪽 하위 트리의 노드의 Key는 현재 노드의 Key보다 커야 한다. BST는 Key를 정렬된 순서로 유지하므로 조회 및 기타 작업에서 Binary search을 활용할 수 있다.

def binary_search(key, node):
    if node is None or node.key == key:
        return node
    elif key < node.key:
        return binary_search(key, node.left)
    else:
        return binary_search(key, node.right)

BST는 n개의 아이템에서 평균 \(O(\log{}n)\), 최악에는 \(O(n)\) 시간 복잡도로 특정 아이템을 찾을 수 있다. 또 inorder traversal를 이용하면 BST에서 순서대로 아이템을 순회할 수 있다. 유독 Depth-first search(DFS)중 inorder traversal만 “iterative로 inorder traversal을 구현하시오.” 같은 문제로 코딩 인터뷰에 더 등장하는 것 같다.

def inorder_traversal(node):
    if node is None:
        return
    inorder_traversal(node.left)
    print node.value
    inorder_traversal(node.right)

BST의 성능은 트리의 균형(balance)와 밀접한 관련이 있다. 균형이 깨져서 한쪽으로 길어지면(skewed), Binary search을 이용하더라도 시간 복잡도가 선형 시간(linear time)에 가까워진다.

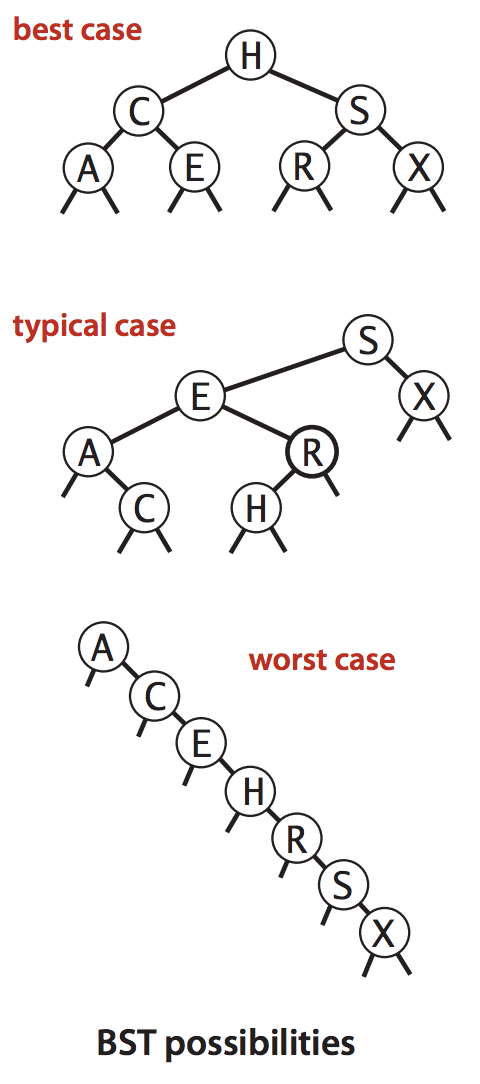^{출처: Robert Sedgewick and Kevin Wayne: Algorithms FOURTH EDITION. Pearson Education, 2011}

Weight 속성의 Search tree

Key가 아닌 Weight 속성을 사용해서 Search tree를 구성하면 특정 index를 \(log_2(n)\) 이내로 찾을 수 있는 리스트 형 자료구조를 구현할 수 있다. Weight 속성을 이용한 BST의 get은 아래와 같다.

public Node get(Node node, int index) {
  while (true) {
    if (node.hasLeft() && index <= node.getLeftWeight()) {
      node = node.getLeft();
    } else if (node.hasRight() && node.getLeftWeight() < index) {
      index -= node.getLeftWeight();
      node = node.getRight();
    } else {
      index -= node.getLeftWeight();
      break;
    }
  }
  return node;
}

삽입 시 Shift가 일어나지 않으므로 Array보다 삽입/삭제가 빠르고 Linked list보다 index 기반 조회가 빠르다.

The following relative performance statistics are indicative of this class:
              get  add  insert  iterate  remove
 TreeList       3    5       1       2       1
 ArrayList      1    1      40       1      40
 LinkedList  5800    1     350       2     325

^{출처: apache/commons/collections4/list/TreeList.html}

Self-balancing BST

BST의 균형 문제를 해결한 Self-balancing BST가 있는데, 수정 시 자동으로 균형을 유지한다.

BST rotation

보통 Self-balancing BST는 각자 전략에 맞춰서 판단한 뒤 회전을 이용해서 균형을 유지한다. BST의 간단한 회전의 예는 다음과 같다.

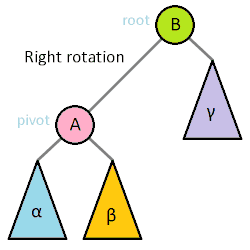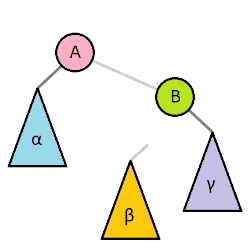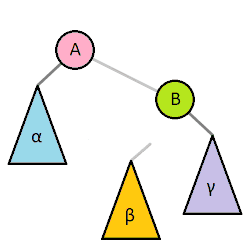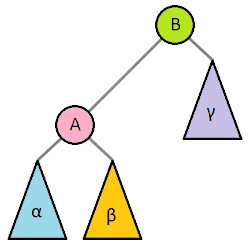^{출처: https://en.wikipedia.org/wiki/Tree_rotation}

AVL tree

AVL tree는 노드의 좌측 하위 트리의 높이(height)와 우측 하위 트리의 높이가 트리의 높이의 차이가 1 이하를 유지한다. AVL tree에서는 수정으로 높이 차이가 1보다 커지면 회전을 이용해서 높이 차이를 1 이하로 유지한다.

^{출처: https://en.wikipedia.org/wiki/AVL_tree}

AVL tree는 HackerRank의 연습문제, Self Balancing Tree를 풀다가 구현했다.

Splay tree

Splay tree는 Splaying이라 부르는 특정 형식의 회전을 이용해서 접근한 노드를 루트로 올리면서 균형을 유지한다. 접근한 노드를 루트로 올리는 Splaying이 다른 동작의 기반 Operation이고 Join과 Split을 구현하기가 쉽다. 자주 접근한 노드가 루트 근처에 있으므로 Cache를 구현하는 데 유용하다.

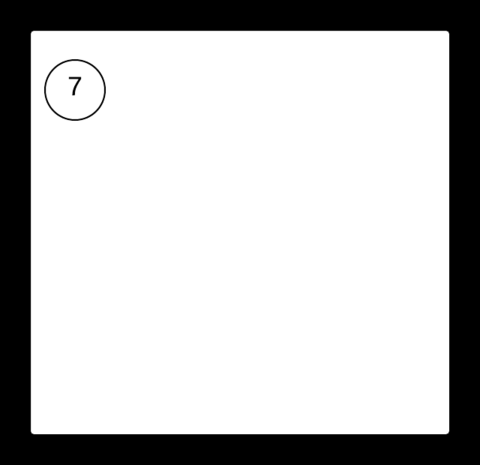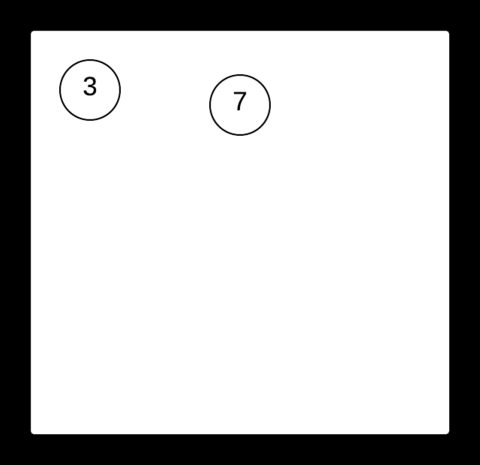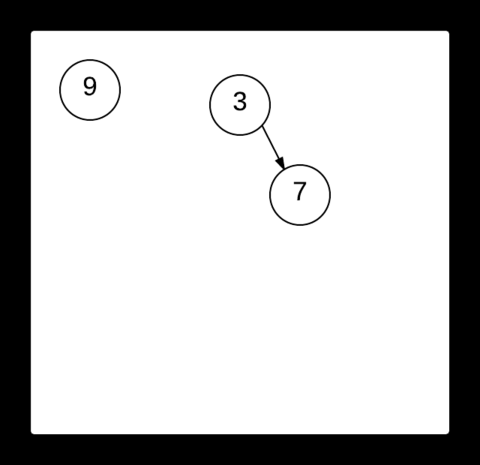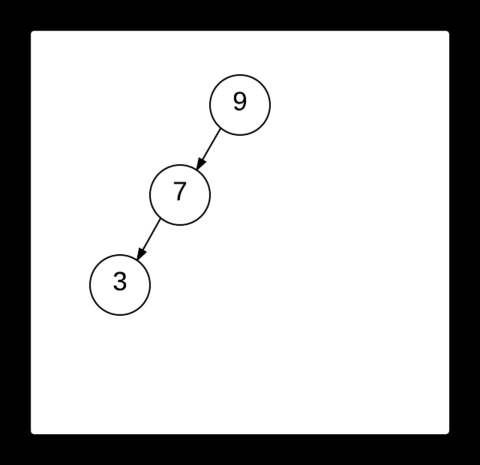^{출처: https://brilliant.org/wiki/splay-tree/}

텍스트 에디터의 동시편집을 위한 RGATreeSplit의 identifier 자료구조를 만드는 데 사용했다. Atom의 동시편집을 위한 모듈인 Teletype-CRDT도 RGATreeSplit을 기반으로 구현되어 있는데, Splay tree를 사용한 것을 참고했다.

Treap

Treap은 Tree와 Heap의 합성어로 균형 유지에 Random priority를 이용한다. Treap의 구조는 Heap 순서로 정렬되어야한다는 요구 사항에 따라 결정된다. 새로운 노드 생성시 Random priority를 할당하고 일반 BST처럼 삽입한 뒤 회전을 이용해서 부모 자식사이에 priority 순서를 맞춘다.

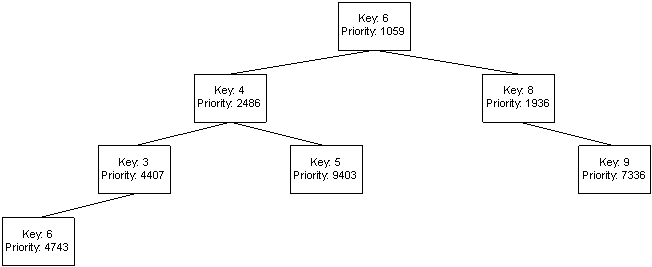^{출처: 340treap.htm}

Treap은 HackerRank의 연습문제, Array and simple queries를 풀면서 Discussions 탭의 대화를 참고해서 구현했다.

B-tree

B-tree는 2-3 tree와 2-3-4 tree 등의 일반화 트리다. 예를 들어 2-3-4 tree는 order가 4인 B-tree이다. B-tree는 BST는 아니다. 2-3 tree는 자식이 2개 또는 3개만 있을 수 있다.

^{출처: indexing.pdf}

B-tree 디자인은 컴퓨터의 Memory hierarchy와 관련 있다. 컴퓨터를 CPU ↔ Cache ↔ Disk로 추상화한다면 Cache에 있는 데이터 접근 속도는 빠르지만, Disk에 있는 데이터 접근 속도는 느리다. 따라서 트리가 Cache가 아닌 Disk에 있다면 I/O 수를 줄이는 게 성능에 유리하다. B-tree는 한 노드가 다수의 자식 노드를 갖고 있으므로(보통 order가 100 이상) Disk I/O 수가 BST보다 작고 블록 스토리지에 유리하다.

Red-black tree

BST 형식이면서 B-tree의 특징을 취한 트리가 Red-black tree(이하 RB tree)이다. RB tree의 Red link를 수평으로 펼치면 2-3 tree에 대응된다.

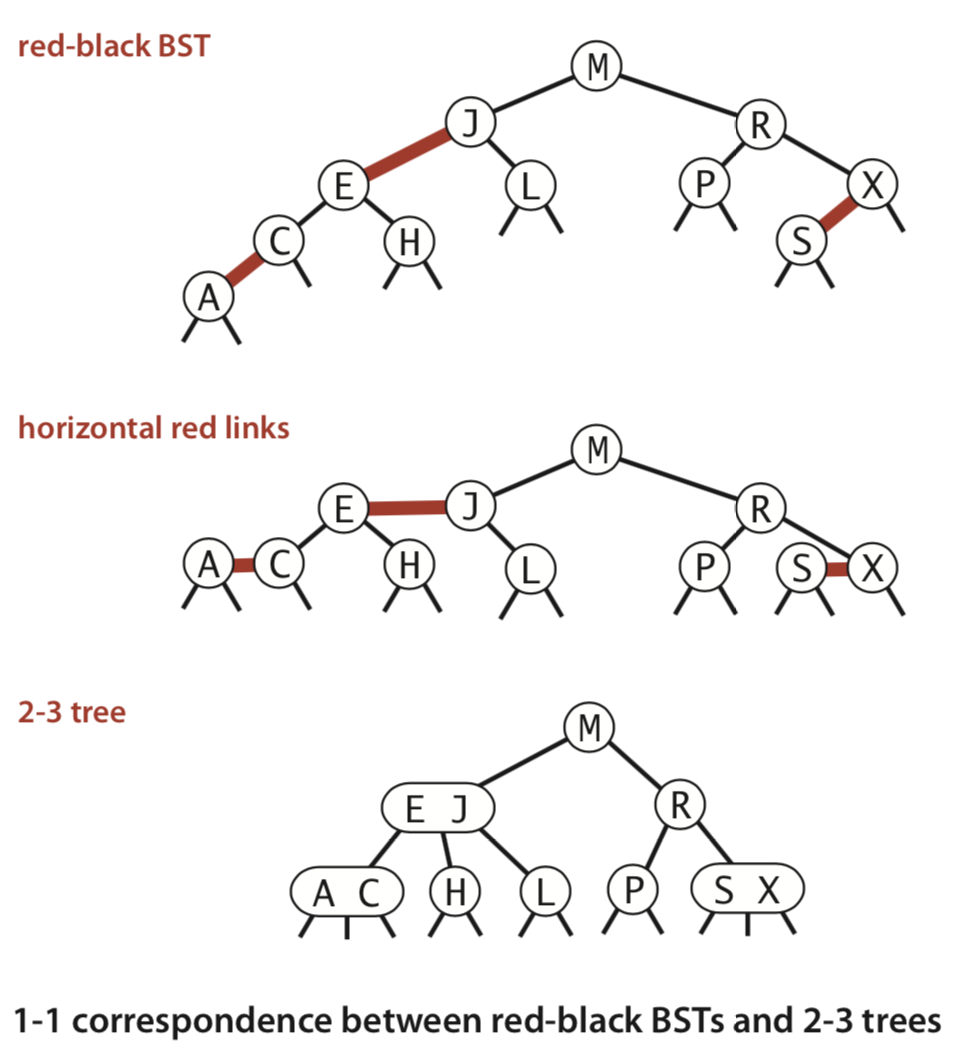^{출처: Robert Sedgewick and Kevin Wayne: Algorithms FOURTH EDITION. Pearson Education, 2011}

RB tree는 노드에 Red 혹은 Black을 표현하는 1bit 플래그가 추가된다. RB tree는 AVL tree와 비교하면 엄격한 균형을 유지하지는 않으므로 검색은 조금 느릴 수 있지만, 수정은 더 빠르다.

Left-leaning red-black tree(이하 LLRB tree)는 세 가지 아이디어를 더해서 RB tree보다 구현하기 쉽게 디자인되어 있다. 자바스크립트에는 자바의 SortedMap처럼 내장 SortedMap이 없어서 구현이 필요했다. 일반 RB tree의 구현은 복잡해서 망설였는데, Firebase JS SDK에서 LLRB tree로 SortedMap을 구현한 것을 참고했다.

B+tree

B+tree는 B-tree와 달리 Leaf 노드를 제외한 노드에는 Key만 있고 Leaf 노드에 Key와 Value가 있다. 그리고 Leaf 노드는 Linked list처럼 서로 연결되어 있다. B+tree는 데이터베이스의 Index를 구현하는 데 자주 사용된다

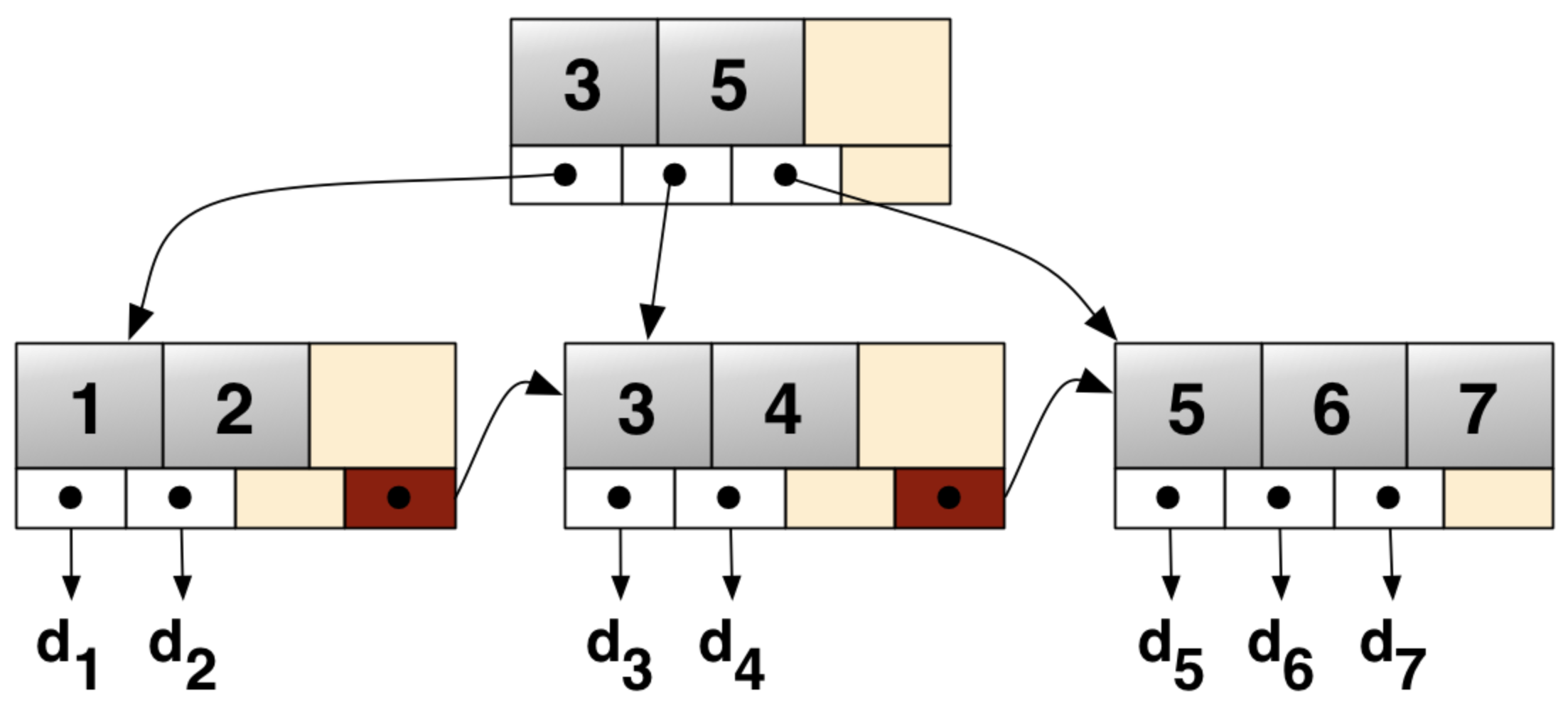^{출처: https://en.wikipedia.org/wiki/B%2B_tree}

B+tree의 Leaf 노드가 연결되어 있어서 JSON-like CRDT의 Array를 구현하는 데 활용했다. 하지만 트리를 디스크에 올려놓고 사용하진 않으므로 RB tree로 변경을 고민하고 있다.

마무리

코딩 인터뷰에서 Search tree 문제를 만나서 당황했던 적도 있다. 지금도 풀라고 하면 못풀 것 같다. 하지만 일하면서 자료구조를 구현해서 사용하는 경험은 즐거웠다. 앞으로도 이런 기회가 있었으면 좋겠다.

참고

← → Top