CS229a - Week 4

Written by hackerwins on June 16, 2019

Motivations

Non-linear hypotheses

Why do we need, you know, neural networks? For many interesting machine learning problems would have a lot more features than just two.

\[g(\theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_1x_2 + \theta_4x_1^2x_2 + ...) \text{ for two features: } x_1, x_2\]

Suppose We have a housing classification.

\[x_1^2, x_1x_2, x_1x_3,...x_1x_{100}\\x_2^2,x_2x_3...x_2x_{100} \\ ...\] \[\text{number of quadratic terms}=\frac{n^2}{2}\]

One thing we could do is include only a subset of these, so if we include only the features x1 squared, x2 squared, x3 squared, up to maybe x100 squared, then the number of features is much smaller. but this is not enough features and certainly won’t let you fit the data set like that on the upper left.

Car detection Problem: the computer sees matrix or grid of pixel intensity values that tell us the brightness of each pixel in the image.

\[50 \times 50 \text{ pixel images} = 2500 \text{ (7500, if RGB)} \\ \text{Quadratic features}(x_i \times x_j): 3 \text{ million features}\]

Neurons and the Brain

Neural Networks origins: Algorithms that try to mimic the brain. Recently computers became fast enough to really run large scale Neural Networks. Modern Neural Networks today are the state of the art technique for many applications.

The way the brain does it is worth just a single learning algorithm(i.g Auditory cortex, Somatosensory cortex).

Neural Networks

Model Representation

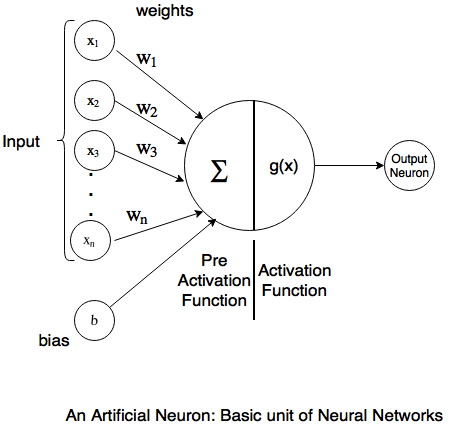
The neuron has a number of input wires, and these are called the dendrites. And a neuron also has an output wire called an Axon. this output wire is what it uses to send signals to other neurons, so to send messages to other neurons. So, at a simplistic level what a neuron is, is a computational unit that gets a number of inputs through it input wires and does some computation and then it says outputs via its axon to other nodes or to other neurons in the brain.

Neuron model: Logistic unit

\[x =\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} \text{, } \theta =\begin{bmatrix} \theta_1 \\ \theta_1 \\ \theta_2 \\ \theta_3 \end{bmatrix} \text{, } h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\]

x_0: bias unit, x_0 = 1
Sigmoid or Logistic activation function.
\theta: “weights” or “parameters”

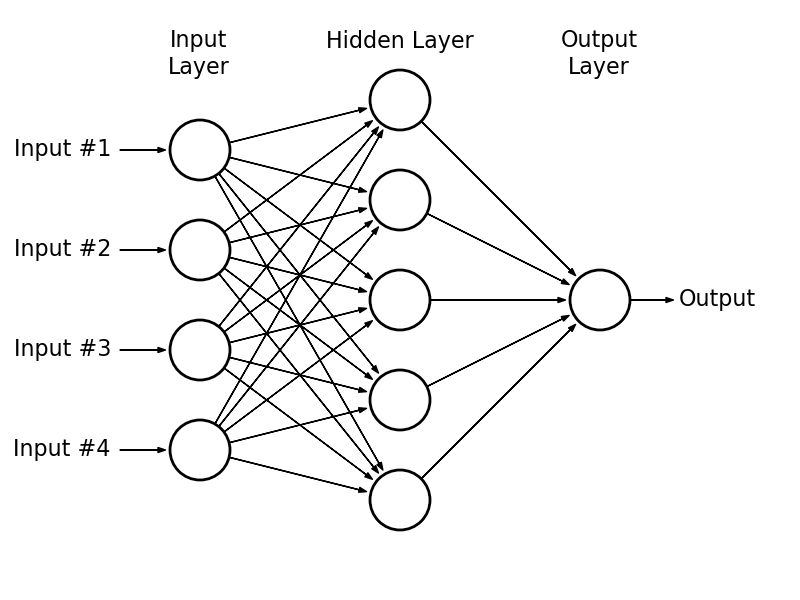
Layer 1: “input layer”
Layer 2: “hidden layer”
Final layer: “output layer”

Neural Network notations

\[\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} \rightarrow \begin{bmatrix} a_1^{(2)} \\ a_2^{(2)} \\ a_3^{(2)} \end{bmatrix} \rightarrow h_\theta(x)\]

a_i^{(j)} = activation of unit i in layer j
\Theta^{(j)} = matrix of weights controlling function mapping from layer j to layer j + 1

\[a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_3 + \Theta_{13}^{(1)}x_3) \\ a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_3 + \Theta_{23}^{(1)}x_3) \\ a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_3 + \Theta_{33}^{(1)}x_3)\] \[h_\theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_{0}^{(2)} + \Theta_{11}^{(2)}a_{1}^{(2)} + \Theta_{12}^{(2)}a_{2}^{(2)} + \Theta_{13}^{(2)}a_{3}^{(2)})\] \[\Theta^{(1)} \in \R^{3\times4}\]

If networks has s_j units in layer j, s_{j+1} units in layer j + 1, then \Theta^{(j)} will be of dimension s_{j+1} \times (s_j + 1)

Forward propagation: Vectorized implementation

\[a_1^{(2)}=g(z_1^{(2)}) \\ z_1^{(2)} = \Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_3 + \Theta_{13}^{(1)}x_3)\] \[x =\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix}\text{ } z^{(2)} = \begin{bmatrix} z_1^{(2)} \\ z_2^{(2)} \\ z_3^{(2)} \end{bmatrix}\] \[z^{(2)} = \Theta^{(1)}x \\ a^{(2)} = g(z^{(2)})\]

Add a_0^{(2)} = 1. (bias)

\[z^{(3)}=\Theta^{(2)}a^{(2)}\\h_\Theta(x) = a^{(3)} = g(z^{(3)})\]

Just to say that again, what this neural network is doing is just like logistic regression, except that rather than using the original features x1, x2, x3, is using these new features a1, a2, a3.

Examples and Intuitions

Neural networks as logical gates

Neural networks can also be used to simulate all the other logical gates. The following is an example of the logical operator ‘OR’, meaning either x_1 is true or x_2 is true or both:

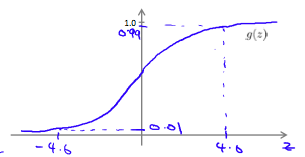
Where g(z) is the following

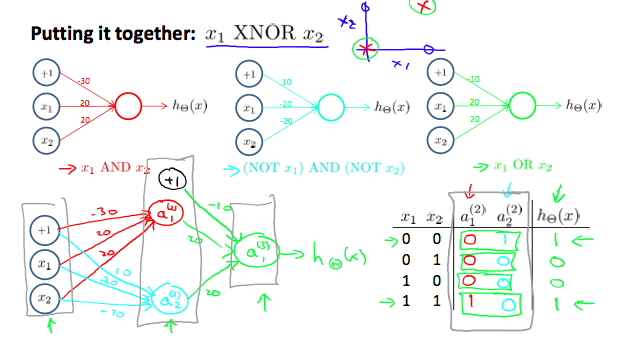
Neural networks as XNOR:

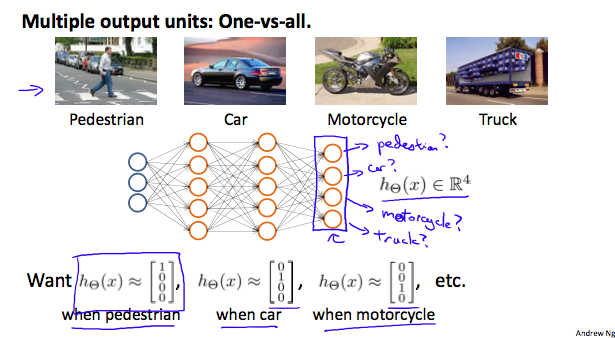
Multi-class classification: One-vs-all

To classify data into multiple classes, we let our hypothesis function return a vector of values. Say we wanted to classify our data into one of four categories. We will use the following example to see how this classification is done. This algorithm takes as input an image and classifies it accordingly:

← → Top