OpSets 요약

“OpSets: Sequential Specifications for Replicated Datatypes (Extended Version).” 읽으면서 정리한 내용

요약

이 논문은 분산 시스템에서 최종적인 일관성(eventual consistency)의 복제 데이터타입(replicated datatype)을 구현한 프레임워크인 OpSets를 제안한다. 또 이런 유형의 데이터타입(CRDT)을 구현하는 알고리즘을 기계적으로 검증한다. 이는 간단하지만 표현력이 뛰어나므로 맵(map), 세트(set), 리스트(list), 텍스트(text), 그래프(graph), 트리(tree) 및 레지스터(register)를 비롯한 다양한 추상 데이터타입을 간단히 적용할 수 있다. 또 데이터타입을 복잡한 데이터 구조를 구성할 수 있다. 복제 알고리즘을 분석하기 위한 OpSet의 기능을 알아보기 위해, 이전부터 간과되었지만 협업 텍스트 편집에서 중요한 정확성(correctness property)에 대해 살펴본다. 정확성을 만족시키지 않는 알고리즘은 텍스트 공동편집시 의도하지 않은 글자가 삽입되는 현상이 나타난다. OpSets를 사용해서 정확성을 정의하고 기존 복제 알고리즘들이 정확성을 충족시키는지 확인한다. 또한 새로운 복제 된 데이터타입을 개발하는 데 OpSets를 사용하는 방법에 대해서 알아본다. 기존에는 잠금장치(Lock)를 사용하지 않고 구현하기 어려웠던 트리에서 원자적 이동 Operation에 대해 알아본다. 이 논문은 이전의 비공식 접근 방식의 모호함을 없애고 추론 오류를 배제하기 위해서 Isabelle/HOL 증명 도구를 사용해서 OpSets를 공식화하고 주요 주장의 정확성에 대해서 기계적으로 증명한다.

1. 도입

공통적인 분산 시스템의 요구 사항은 여러 노드가 공유 데이터에 동시에 접근하고 조작하는 것이다. 예를 들어, 노트북을 사용하는 기자의 공유 텍스트 문서 작업부터 공통 데이터베이스를 조작하는 웹 서버들이 있다. 이때 공유 데이터가 일정한 일관성을 보장하도록 하는 것이 중요하다. 예를 들어 serializability 또는 linearizability와 같은 강력한 일관성 모델(strong consistency models)은 실제로 복제되고 동시에 실행되는 경우에도 시스템이 연속적으로 실행되는 단일 노드처럼 작동한다. 이 모델의 단점은 모든 동작이나 트랜잭션이 완료되기 전에 네트워크 통신을 기다려야 한다는 것이다. 따라서 일관성이 강한 시스템에서는 노드가 오프라인이거나 다른 노드들과 단절된 상태(network partition)에서 작업을 진행할 수 없다.

반면에 최종적인 일관성은 각 참여자가 오프라인 상태에서 공유 데이터 구조의 로컬 복사본(replica)을 수정할 수 있지만 그 정의가 빈약하다. “공유 상태에 대한 새로운 업데이트가 없으면 모든 노드의 데이터는 결국 동일하다”에서 “새로운 업데이트가 없으면”이라는 전제는 공유 상태가 지속적으로 수정되면 (예를들어 시스템이 절대로 정지되지 않는 경우) 참이 될 수 없다. 또한 최종적인 일관성의 정의에는 최종 상태가 적합한지 여부를 명시하지 않았다.

CRDT는 최근 몇 년 동안 주목을 받아온 복제된 상태의 추상화이다. CRDT의 주요 정확성(correctness property)은 수렴(convergence)이다. “두 개의 복제본이 동일한 업데이트들을 적용 할 때, 동일한 복제본이 다른 순서로 업데이트를 적용하더라도 동일한 상태로 수렴한다. 이는 최종적인 일관성보다 단단하지만, 수렴 상태가 정확히 무엇인지를 정의하지는 않았다.

이 논문은 복제 된 데이터 형식적 의미론(Formal semantics)을 정의하고 동시에 데이터에 접근하거나 조작하기 위한 알고리즘에 대한 새로운 접근 방식, Operation Sets(OpSets for short)를 제안한다. OpSets은 일부 업데이트들이 적용된 후 복제본의 허용된 상태를 정확하게 정의하는 실행 가능한 스팩이다. 이 논문의 공헌은 다음과 같다.

• 2절에서는 동시 편집 데이터 구조의 일관성에 대한 지정 및 추론을 위한 간단한 추상화 OpSet을 소개한다.
• 3절과 5절에서는 OpSet의 다양한 추상 데이터타입(맵, 세트, 리스트, 텍스트, 그래프, 트리 및 레지스터)를 소개하며, 이 스펙이 간단하고 정확하다는 점에 대해 알아본다.
• 4절에서는 OpSet를 사용하여 기존 알고리즘을 추론하는 방법을 알아본다. 이 분야의 선행 연구에서 간과 되어온 협업 텍스트 편집을 위해 중요한 정확성(correctness property)에 대해 살펴본다. 이 논문 저자는 OpSet 스펙이 정확성을 올바르게 정의한 첫 번째라고 주장한다. 텍스트 편집 CRDT에서 정확성을 만족시키지 못하는 몇 가지 다른 사례들을 살펴본다.
• 5절에서는 OpSet를 사용하여 새로운 복제 된 데이터타입을 개발하는 방법에 대해 알아본다. 특히 트리 CRDT에서 원자 이동 Operation을 정의하는 방법을 소개한다. 이 작업은 트리 내의 새 위치로 하위 트리를 이동하거나 맵에서 키의 이름을 바꾸거나 리스트에서 항목의 순서를 변경하는 데 사용할 수 있다. OpSets 접근 방식은 그 동안 잠금장치(Lock) 없이 구현할 수 없던 작업을 간단하게 정의할 수 있다.
• Isabelle/HOL 증명 도구를 사용하여 OpSets를 공식화하고 이 논문의 주요 주장의 정확성에 대한 기계화 된 증명을 산출한다. 특히 공동 텍스트 편집의 최근 스펙인 Attiya 보다 더 엄격하게 입증한다. 기계화 된 교정을 사용함으로써 이전의 비공식적 인 접근 방법의 모호성 없이 텍스트 수정에서 발생할 수있는 추론 오류를 배제한다.

2. OpSets 접근방식

OpSets 접근방식은 복제 된 데이터 시스템의 일관성을 설명하기 위한 간단한 추상화이다. 이 절에서는 일반적인 접근 방식에 대해 알아보고 3절, 5절에서 구체적인 데이터 구조와 스펙을 설명한다.

2.1 시스템 모델

대상 시스템은 네트워크에 연결된 노드 세트으로 구성된다. 각 노드는 관계형 데이터베이스(row를 갖은 테이블), 텍스트 문서(문자 시퀀스), 벡터 그래프 문서(그래프 개체의 레코드 트리), 파일 시스템(디렉토리, 파일의 트리) 등의 데이터에 접근한다.

새 노드는 언제든지 추가 할 수 있으며 사전에 노드 세트을 알 필요는 없다. 노드는 모바일 장치와 같이 일시적으로 다른 노드와 통신 할 수 없다고 가정한다. 노드는 오프라인에서도 언제든지 공유 데이터(shared data)에 접근할 수 있어야한다. 따라서 각 노드는 공유 데이터의 로컬 사본(copy)을 가지며, 다른 노드와의 통신 또는 조정을 기다리지 않고 공유 데이터를 읽고 수정할 수 있다.

노드가 공유 데이터를 수정하면 변경 사항을 Operation으로 기록한다. 예를 들어, 텍스트 문서의 특정 위치에 삽입을 Operation으로 표현한다. 각 노드는 로컬에 Operation의 세트, OpSet을 관리한다. 노드가 공유 데이터를 변경하면 OpSet에 해당 Operation을 추가하고 Operation이 포함된 메시지를 다른 노드에 전송한다. 노드가 다른 노드에서 메시지를 수신 하면, 해당 메시지의 Operation이 수신자의 로컬 OpSet에 추가된다. Operation은 전체 과정에서 변경되지 않는다(Immutable).

네트워크의 신뢰성에 대해서는 아무런 가정을 하지 않는다. 메시지는 손실(lost)되거나 중복(duplicate)되거나 임의 순서(reordered)로 전달 될 수 있다. 실제 네트워크의 특성을 반영하여 가능한 경우 손실 된 메시지를 재전송한다고 가정하지만 (예 : TCP 사용) 네트워크 또는 노드 오류로 인해 메시지가 영구적으로 손실 될 수 있다. 각 노드의 OpSet은 단조롭게(monotonically) 증가하는 Operation 세트이므로 두 통신 노드는 표준 조합 연산자 ∪(Union)을 사용하여 OpSets를 병합 할 수 있다. OpSets의 합집합은 교환 법칙(commutative), 결합 법칙(associative), 멱등 법칙(idempotent)이 적용 되므로 통신중인 노드가 동일한 OpSet 내용으로 수렴(converge)된다.

각 Operation은 고유 ID를 갖고 있으며, 모든 노드는 다른 노드와 통신하지 않고 새 ID의 생성이 가능하며 Operation ID는 전체 시스템에서 순서를 매길 수 있다고 가정한다(total ordering). 램포트 시계(Lamport timestamp)를 ID로 사용하면 이 요구 사항을 쉽게 충족시킬 수 있다. 램포트 시계는 다음과 같이 (counter, nodeID)로 구성된 쌍이다.

• counter는 정수(integer)다. Operation ID 생성시, 로컬 OpSet의 기존 Operation ID 중 최대값을 하나 증가시켜서 할당한다.
• nodeID는 ID를 생성하는 노드를 고유하게 식별하는 문자열이다(예: UUID).

서로 다른 노드가 동일한 카운터 값을 갖는 ID가 생성될 수도 있지만, 각 노드는 엄격하게 단조롭게 증가하는 카운터 값으로 ID를 생성하므로 ID는 전역적으로 고유하다(nodeID가 고유하므로). Operation ID에 대한 전체 순서는 다음과 같이 정의한다.

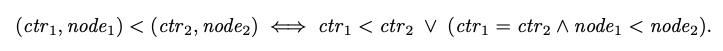
2.2 OpSet 해석하기

대부분의 Operation 기반 CRDT는 노드의 로컬 상태가 Operation에 의해 어떻게 조작되는지를 기술하지만 이 논문은 복제된 데이터 타입을 다른 방식으로 설명한다.

OpSets 접근 방식은 공유 데이터 구조가 직접 조작되지 않는다. 대신 OpSet O를 해석 함수[-]를 사용해서 공유 데이터의 현재 상태인 [O]를 반환한다. 해석 함수(interpretation function)는 순수 함수, 즉 결정적(deterministic)이고, 부수효과가 없으므로(no side effect), 그 결과는 O에만 의존한다. 시스템의 모든 노드는 동일한 해석 함수를 사용한다.

결과적으로 두 노드가 동일한 OpSet O에 대해서 공유 데이터의 [O]에 대한 값도 동일하다. 이 구성은 최종적인 일관성(eventual consistency)을 보장한다. 두 노드가 동일한 OpSet으로 수렴하므로 OpSet에서 결정적으로 파생 된 모든 데이터도 수렴한다(convergence).

원칙적으로 결정적 함수(deterministic function)는 해석 함수로 사용될 수 있다. 그러나 CRDT의 의미론(semantics)을 정의 할 때(3절과 5절 참조) 한 번에 하나의 Operation을 해석하도록 [-]를 분리하는 것(specialize)이 유용했다.

OpSet O는 페어(id, op)의 세트이다. 여기서 id는 고유 한 Operation 식별자이고 op는 발생한 수정 내용의 설명이다. 2.1절에서 설명한 것처럼 식별자는 전체 순서가 보장된다고 가정한다. 임의의 OpSet에 대해서 모든 Operation들은 Operation ID에 의한 오름차순 순서가 있음을 알 수 있다. 해석 함수를 하나씩 적용할 때 각 Operation의 의미론을 정의할 수 있다.

형식적으로 OpSet O의 해석 함수 [O]는 다음과 같이 정의 한다.

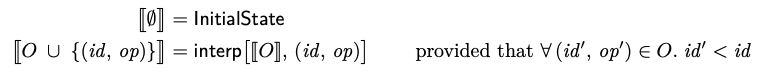
여기서, interp[S, (id, op)]는 상태 S의 Operation (id, op) 해석이고, InitialState는 복제 데이터 타입의 최소 상태(예를 들어, 빈 트리 또는 빈 리스트)이다. 즉, S가 id보다 작은 식별자를 가진 모든 Operation을 해석 한 결과라면, interp[S, (id, op)]는 (id, op)가 추가 된 OpSet의 해석이다. 예를 들어, id1 <id2 <id3 인 경우 다음과 같다.

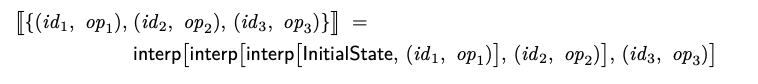
OpSet의 Operation 순서가 고유하므로, 해석 interp[S(id, op)]가 결정적이라면 OpSet 해석 함수 [-]도 결정적이다.

2.3 잘못된 순서로(out of order) 메시지 수신하기

많은 컴퓨팅 시스템들은 Operation들을 전체 순서로 추가하고 그 순서대로 실행 한다는 규칙을 기반으로 한다. 예를 들어, 직렬화 트랜잭션(serializable transactions)과 상태 머신 복제(state machine replication)는 이 접근법을 따른다. 그러나 2.2절에서 설명한 OpSet 해석은 대부분의 시스템보다 약한 순서 개념(weaker notion of ordering)을 사용한다는 점을 주목하자.

직렬화 트랜잭션 이나 상태 머신 복제에서 트랜잭션/Operation의 특정 상태에서 실행한 결과는 내구성(durable)이 있어야 한다. 따라서, 특정 트랜잭션 Ti를 실행하기 전에, 시스템은 Ti보다 낮은 ID를 갖는 보류중인 트랜잭션 이 없는지 확인해야 한다(Ti보다 먼저 실행 되야함). 그렇지 않으면 이후 ID가 낮은 트랜잭션이 도착하면 Ti가 실행 된 상태가 무효화되기 때문이다. 그러나 이 전제 조건을 보장하는 것은 비용이 많이 든다. 6.1절에서 살펴보지만 적어도 노드 쿼럼과의 통신이 필요하다. ID가 램포트 시간이면 모든 단일 노드와의 통신이 필요하다. 많은 노드가 오프라인인 경우에는 시스템은 어떤 트랜잭션도 실행할 수 없다. 반대로 2.1절의 시스템 모델은 모든 노드가 오프라인 일 때도 노드가 항상 공유 데이터를 읽고 수정할 수 있다. 또한 네트워크에서 순서 보장을 가정하지 않는다. 특정 노드의 OpSet O에 특정 Operation (id1, op1) ∈ O를 만족할 때 (id2, op2)를 포함하는 메시지를 수신 할 수 있는데, 여기서 id2 <id1 즉, 나중에 도착한 Operation을 OpSet 해석 [O]의 기존 Operation (id1, op1)보다 먼저 적용하는 것이 필요할 수 있다.

OpSet 모델에서 이러한 비 순차적 인 Operation의 전달은 문제가 되지 않는다. Operation의 수신 순서는 OpSet O에는 아무런 영향을 미치지 않으며, 해석 함수가 순수하고 부수효과가 없다고 가정하기 때문에 해석 작업은 새로운 Operation이 O에 추가 될 때마다 항상 다시 계산된다(XXX: 실제품에 사용이 가능할까?). 해석 함수는 일련의 Operation을 해석 할 때 예상되는 결과를 정의하는 실행 가능 스펙이다. 이 방식으로 복제 된 데이터타입을 구현하면 두 가지 중요한 이점이 있다.

• 다른 CRDT 알고리즘 정의와 다르게 해석 함수 interp[S(id, op)]는 다른 Operation과 관련하여 commute할 필요가 없다. 어떤 순수한 함수도 사용할 수 있다. 이는 3절과 5절에서 볼 수 있듯이 Operation 해석을 기술하는 일이 훨씬 간단해진다.
• 기술한 각 데이터타입의 구현의 존재를 스펙 자체로 보장 할 수 있다. 이는 구현할 수 없는 공리적 명세와는 달리, 공리적 설명을 만족시키는 구현이 존재 함을 입증하기 위해 추가 작업이 필요하다.

노드가 잠재적으로 동일한 하위 Operation 세트을 반복적으로 적용하기 때문에 순수 OpSet 해설은 실제 구현보다 성능이 저하 될 수 있다. 따라서 OpSet 기반 스펙을 만족하고 CRDT의 효율적인 (그리고 아마도 가장 복잡한) 알고리즘의 구현은 4절에서 알아본다.

OpSet 모델을 기반으로 실용적인 JavaScript CRDT 구현체를 개발했고 몇 가지 장점을 발견했다. 예를 들어, 문서의 모든 편집 버전이 해석이므로 문서의 편집 내역을 쉽게 검사 할 수 있다. 특정 작업의 하위 세트 또한, OpSets를 사용하면 누락 된 Operation이 이전에 단절된 노드의 OpSets에 재전송되어 추가 될 수 있으므로 네트워크 파티션, 장애로부터 복구 할 수 있는 간단한 메커니즘을 제공한다. 하지만 이 구현의 세부 사항은 이 논문의 범위를 벗어난다.

3. 리스트, 맵, 레지스터, 그래프 정의하기

3장에서는 일반적 데이터구조(예: 사용자 지정 키와 값의 맵), 리스트(값의 선형 순서)과 같은 예제 의미를 정의하여 OpSets를 구체적으로 구현한다. 맵 데이터 타입은 세트도 표현할 수 있다(키를 세트의 구성원으로 사용하고 값을 무시). 리스트 데이터 유형은 텍스트로 표현할 수 있다(각 문자를 리스트 요소에 매핑). 리스트와 맵 모두 값은 기본형 데이터(숫자, 문자열)나 다른 맵 또는 리스트에 대한 참조 이다. 이러한 참조를 사용하여 객체 지향 프로그래밍 언어에서 처럼 임의의 객체 그래프를 구성 할 수 있다. 5장에서는 이 객체 그래프를 트리로 제한하는 방법을 알아본다.

맵의 키와 리스트의 요소는 다중 값 레지스터(multi-value register)로 처리한다. 즉, 동일한 맵 키 또는 리스트 요소에 여러 값이 동시에 할당되는 경우, 쓰여지는 모든 값을 유지한다. 이 때문에, 맵 키 또는 리스트 요소를 읽어는 일은, 유저가 명시적으로 병합할 수 있도록 복수의 값을 반환할 수 있다. 맵 키 또는 리스트 요소에 새 값을 할당하면 이전의 모든 값(casually preceding value)을 덮어 쓴다. last-writer-wins(동시에 작성된 값 중 하나를 승자로 선택)와 같은 레지스터 동작을 쉽게 정의 할 수 있다.

3.1 Operation 생성하기

일반적 데이터 구조의 OpSet에는 다음과 같이 6가지 유형의 Operation이 포함된다.

• (id, MakeMap)은 id로 식별되는 비어있는 새 맵 객체를 만든다.
• (id, MakeList)는 id로 식별되는 비어있는 새 리스트 객체를 만든다.
• (id, MakeVal(val))는 id로 식별되는 기본형 값 val(i.g.: 숫자, 문자열 또는 boolean)을 할당한다. 이 Operation은 값을 감싸는데 사용하며 값으로 기본형 혹은 맵 또는 리스트에 대한 참조로 갖는다.
• (id, InsertAfter(ref))는 id로 식별되는 새 요소를 만들어서 리스트에 삽입한다. ref가 MakeList Operation의 ID 인 경우, 새로운 요소가 리스트의 head에 삽입된다. 혹은 ref는 기존 리스트 요소의 ID(예: InsertAfter Operation)이어야 하며, 이 경우 새 리스트 요소는 참조한 요소 바로 다음에 삽입된다. InsertAfter Operation에서는 값을 새 요소에 할당하지 않고 이는 Assign Operation에 의해 수행된다.
• (id, Assign(obj, key, val, prev))는 맵의 키에 새로운 값을 할당한다(obj가 이전 MakeMap Operation의 ID 인 경우) 또는 list 요소(obj가 MakeList Operation). 맵 할당의 경우 key는 업데이트 할 사용자 지정 키이며 문자열 또는 정수와 같은 기본 값이 된다. 리스트의 경우, key는 갱신 할 리스트 요소의 ID(즉, 이전의 InsertAfter Operation의 ID)이다. val은 값의 ID이며 MakeMap, MakeList 또는 MakeVal Operation을 식별 할 수 있다. prev는 동일한 객체의 동일한 키에 대한 이전 Assign Operation 들의 ID 세트이며 현재 Operation으로 덮어 쓴다.
• (id, Remove(obj, key, prev))는 맵에서 키-값 쌍을 제거하거나 리스트에서 요소를 제거한다. 할당과 마찬가지로 obj는 업데이트한 객체를 생성 한 이전 MakeMap 또는 MakeList Operation의 ID이며 key는 제거할 키 또는 리스트 요소를 식별한다. prev는 동일한 객체의 동일한 키에 대한 이전 Assign Operation의 ID 세트이며 현재 Operation에 의해 제거된다.

위 Operation 생성의 의사 코드는 부록 A에 있다.

3.2 Operation 해석하기

2.2절에서 주어진 순차적 OpSet 해석을 사용한다. map 및 list 데이터 구조의 현재 상태를 인코딩하기 위해 관계 페어(E, L)를 사용한다.

• 요소 관계 E ⊆ (ID × ID × (ID ∪ Key) × ID): 맵 키와 리스트 요소에 현재 할당 된 값을 포함하는 4-튜플 세트. (id, obj, key, val) ∈ E이면 id를 가진 Assign Operation은 obj를 가진 객체를 업데이트하여 val 값을 map key 또는 list element key에 할당한다. Obj가 리스트 오브젝트를 참조하면, key는 리스트 관계 L에있는 요소의 ID이다(아래 참조). Obj 객체를 참조하는 경우 문자열이나 정수와 같은 기본형을 키로 사용할 수 있다.
• 리스트 관계 L ⊆ (ID × (ID ∪ {⊥})): 리스트 요소의 순서를 나타내는 페어의 세트이다. (prev, next) ∈ L이라면, prev를 갖는 리스트 요소 바로 다음에 ID가 next 인 요소가 뒤따라 온다. (last, ⊥) ∈ L을 사용하여 리스트 요소에 마지막임을 알 수 있다. head는 리스트 obj의 첫 번째 요소이고 (obj는 리스트를 생성 한 MakeList Operation의 ID) (obj, head) ∈ L을 가진다.

초기에는 두 관계가 비어 있다. 즉, [∅] = InitialState = (∅, ∅)이다. 그리고 다음과 같이 여섯 가지 Operation 유형의 해석을 정의한다.

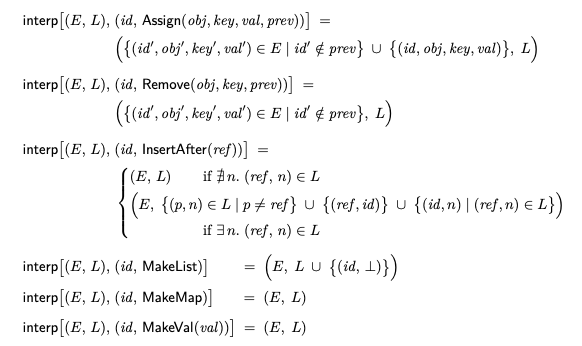
Assign, Remove의 해석은 E만 업데이트하고 L은 변경하지 않는다. 반대로 InsertAfter와 MakeList의 해석은 L만 업데이트 한다. Assign, Remove 해석은 튜플을 인과 관계로 이전 Assign(prev의 ID가 ID로 표시되는 튜플)에서 제거하지만 동시 할당의 튜플은 변경하지 않는데 이는 다중 값 레지스터의 동작이다. last-writer-wins 레지스터가 필요한 경우 id’ ∈/ prev 조건을 obj’ != obj ∨ key’ != key로 변경하면 동일한 객체 ID와 키를 가진 기존 튜플을 제거 할 수 있다.

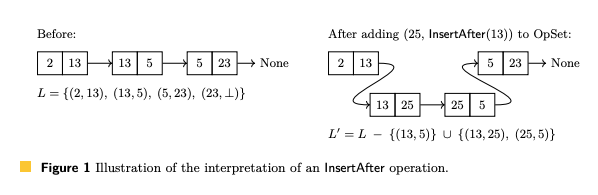
InsertAfter의 해석은 그림 1 에서처럼 링크 된 목록에 삽입하는 것과 유사하다. 예를 들어, (id, InsertAfter(ref))를 해석하기 위해서, (ref, next) ∈ L가 주어지면, L에서 페어 (ref, next)을 제거하고 페어 (ref, id)과 (id, next)를 L에 추가한다. 따라서 새 리스트 요소 id가 ref와 next 사이에 삽입된다.

L은 축소되지 않으며 InsertAfter Operation을 해석하면 커진다. 리스트의 요소가 Remove Operation에 의해 제거되면 요소 관계 E의 리스트 요소에서 값은 제거되지만 요소는 tombstone(삭제 표시)으로 L에 남아 있기 때문에 동시에 발생한 InsertAfter Operation에서 여전히 해당 값을 찾을 수 있다. 따라서 사용자의 관점에서 E 요소 관계에 적어도 하나의 연관된 값이 있으면 리스트 요소만 존재한다. 연관된 값이 없는 모든 리스트 요소는 무시되어야한다.

4. 텍스트 편집 병합하기

3장에서 설명한 데이터타입은 광범위한 애플리케이션에 사용할 수 있다. 예를 들어 리스트 데이터 타입을 사용하여 협업 텍스트 편집기를 구현할 수 있다. 텍스트를 개별 문자 리스트로 처리하고 모든 편집을 리스트에 삽입 또는 삭제 Operation의 순서로 표현한다.

협업 텍스트 편집 문제는 OT와 CRDT라는 두 가지 주요 접근법으로 연구되었다. 6장에서 알아본다. 이제 협업 텍스트 편집에 대해 이전 작업에서 고려하지 않은 시나리오에 대해 알아본다.

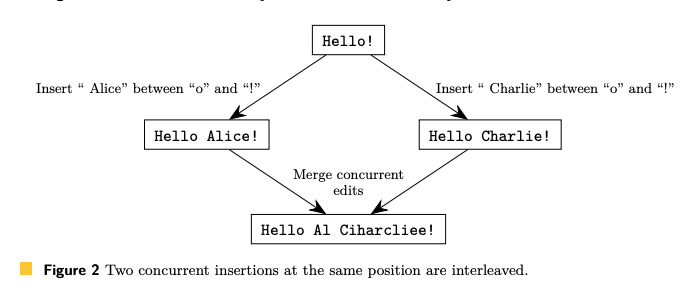
그림 2의 예제에서는 두 명의 사용자가 초기 상태가 “Hello!”라는 텍스트 문서를 동시에 편집하고 있다. 왼쪽 사용자가 “Hello Alice!”로 변경하고 오른쪽 사용자는 문서를 “Hello Charlie!”로 변경한다. 동시 편집 내용이 병합되면 알고리즘에 따라 “Alice”와 “Charlie”의 두 삽입이 문자별로 임의로 인터리빙(interleaving)되면 뜻이 모호한 문자가 된다. 동시 삽입이 단 하나의 단어가 아니라 전체 단락이나 섹션이라면 문제는 더욱 심각한데, 사용자의 삽입을 인터리빙하면 대부분 이해할 수 없는 텍스트가 남아서 다시 작성해야 한다. 그림 2의 병합은 정상 동작은 아니지만 이런 인터리빙 삽입을 제외하는 협업 텍스트 편집의 공식 스펙은 없다.

정리 1. Attiya et al.의 협업 텍스트 Astrong 스펙은 그림 2의 결과가 된다. 즉, 동시 삽입을 동일한 위치에 인터리빙하는 알고리즘은 Astrong 스펙을 만족시킨다. 또한 텍스트 편집 CRDT 알고리즘 인 Logoot 및 LSEQ도 이 결과가 반영된다.

증명. 각 문자를 전체 정렬한 식별자 공간(total ordered identifier space)에서 위치를 할당하는 아이디어에 기반한 각각의 정의에서 식별자의 순서가 문서의 문자 순서와 일치한다. 새로운 문자가 삽입되면 이전 문자와 후속 문자의 식별자 사이에 있는 식별자가 할당된다. 그러나 동일한 전임-후임 요소의 Operation을 가진 동시 삽입이 수행 될 때 이러한 삽입은 임의로 정렬된다. 따라서 동일한 전임-후임 요소 내에서 반복되는 삽입은 임의로 인터리빙 될 수 있다.

또한 Logoot와 LSEQ의 오픈 소스 구현을 사용하여 테스트를 수행했을 때 이러한 인터리빙이 실제로 발생하는 것을 관찰했다.

더 나은 방법은 특정 사용자의 모든 삽입을 연속 시퀀스로 유지해서 문자를 인터리빙하지 않고 병합하는 것이다. 이 조건에서는 그림 2의 예가 “Hello Alice Charlie!”또는 “Hello Charlie Alice!”라는 두 가지 병합된 결과가 된다. 이 두 결과 간의 선택은 임의적이다. 한 사용자의 삽입이 다른 것보다 먼저 오기 위한 사전 요구 사항이 없기 때문이다.

정리 2. 3절의 리스트 스펙은 동시 삽입의 인터리빙을 허용하지 않는다. 즉, 한 사용자가 문자 시퀀스 <x1, x2,. . . , xn> 삽입하고 다른 사용자는 동시에 문자 시퀀스 <y1, y2,. . . , ym>을 같은 위치에 삽입한 경우 병합 문서에는 문자 시퀀스 <x1, x2,. . . , xn, y1, y2,. . . , ym> 또는 문자 시퀀스 <y1, y2 ,. . . , ym, x1, x2,. . . , xn> 의 결과가 된다.

증명. Isabelle/HOL 증명 도구를 사용하여 리스트 스펙과 정리 2를 형식화했다. 형식 증명 구현은 부록 C.3에 요약했다.

그림 3은 인터리빙의 제거 이유를 설명한 그림 2와 유사한 편집 시나리오지만 “Alice”와 “Charlie”의 삽입은 각각 “Al”과 “Ch”로 단축했다. 이 예제에는 여섯 가지 가능한 방법으로 정렬 할 수 있는 네 가지 삽입 Operation( “A”, “l”, “C”, “h”)이 있다. 그러나 6가지 동작의 결과는 ChAl 또는 AlCh 두 가지 결과 만 가능하며 CAhl 또는 AChl과 같은 인터리빙은 발생하지 않는다.

실제로 최종 결과는 각각 “A”와 “C”를 삽입하는 Operation의 상대적 순서에만 의존한다. 다른 모든 Operation은 결과에 영향을 미치지 않고 재정렬 될 수 있다. 따라서 삽입 된 문자열이 2자보다 길더라도 상대 순서는 첫 번째 문자의 ID에만 의존한다. 나머지 문자도 초기 문자 뒤에 온다.

4가지 Operation의 결과는 6가지 문자 순서만 있고 4가지 문자 순서는 없는데, 식별자에 대한 램포트 시계 정렬은 인과 관계 순서의 선형 확장이기 때문이다(2.1 절에 설명한). 이 예에서는 텍스트가 왼쪽에서 오른쪽으로 입력된다고 가정한다(즉, “A”는 항상 “l”앞에 삽입되고 “C”는 “h”앞에 삽입). 이것은 “l”을 삽입하는 Operation의 ID가 “A”삽입보다 크고, “h”삽입이 “C”삽입보다 커야 함을 의미한다.

정리 3의 OpSet 리스트 스펙은 Attiya et al의 Astrong 스펙보다 엄격하다. 즉, 3절에 주어진 리스트 스펙을 만족시키는 알고리즘도 Astrong을 만족하지만 그 반대는 성립하지 않는다.

Astrong 스펙을 Isabelle/HOL로 형식화하고 3절의 리스트 스펙을 실행할 때마다 Astrong의 모든 조건을 충족한다는 기계적으로 검증 된 증거를 제시한다. 공식 증명 구현은 부록 C.5에 요약했다. 스펙이 엄격하고 강하다는 사실은 정리 1과 2를 따른다.

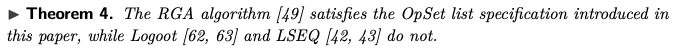
정리 4 : RGA 알고리즘은 이 논문에서 소개한 OpSet리스트 명세를 만족시키는 반면, Logoot와 LSEQ는 그렇지 않다.

증명. 부록 C.4에서 설명한대로 RGA가 우리의 명세를 만족 시킨다는 것을 증명하기 위해 Isabelle/HOL을 사용한다. Isabelle/HOL의 RGA 구현은 이전 연구의 형식화를 기반으로한다. Logoot와 LSEQ가 스펙을 만족시키지 못한다는 사실은 정리 1과 2를 따른다.

5. 복제 된 트리 데이터타입

3장에서는 복제 된 객체 그래프 데이터타입의 OpSet 사양을 제시했는데, 모든 맵 또는 리스트 객체는 고유 한 ID(즉, 객체를 만든 MakeMap 혹은 MakeList Operation의 ID)를 가지며 객체는 이 ID를 사용하여 서로를 참조 했다.

이제 이 모델을 기반으로 객체 그래프가 항상 트리가 되도록 제한하는 방법을 알아보자. 트리는 모든 vertex가 정확히 하나의 parent(root 제외)를 갖고 parent 관계에 사이클이 없는 그래프이다. 트리 데이터타입은 많은 애플리케이션에서 유용하다. 예를 들어, 파일 시스템(디렉토리 및 파일로 구성)과 XML 또는 JSON 문서가 트리이다. 이 트리의 branch 노드는 맵 또는 리스트 일 수 있으며 리프 노드는 기본형 값(MakeVal Operation로 래핑 됨)이다.

5.1 Move Operation 문제

트리 데이터를 사용하는 애플리케이션에서 종종 필요한 작업중 하나는 트리 내의 새 위치로 하위 트리를 이동하는 것이다.

• 파일 시스템에서 디렉토리 이름 변경은 디렉토리 노드를 이전 이름에서 새 이름으로 이동하는 것으로 표현할 수 있다. 마찬가지로 디렉토리를 새 경로로 이동하기도 한다.
• 벡터 그래픽 애플리케이션에서 여러 객체를 논리 단위로 그룹화하는데, 그룹을 나타내는 새 branch 노드를 만든 다음 개별 객체를 해당 그룹 노드의 하위 노드로 이동하여 표현한다.
• To-do list 애플리케이션에서 사용자는 리스트의 순서를 사용하여 우선 순위를 나타내며 항목을 drag&drop으로 순서를 변경한다. 항목 재정렬은 항목을 리스트 내의 새로운 위치로 이동하는 것과 같다.

이전 위치의 하위 트리를 삭제하고 새 위치에서 다시 작성하여 Move Operation을 기본적(naively)으로 표현할 수 있다. 그러나 두 명의 사용자가 이 프로세스를 동시에 수행하는 경우 결과 트리에는 이동 된 하위 트리에 두번 복제 된다. 이는 위에 제공된 모든 애플리케이션에서 바람직하지 않다. 따라서 동시 이동의 경우 중복 객체를 생성하지 않는 Atomic Move Operation이 필요하다.

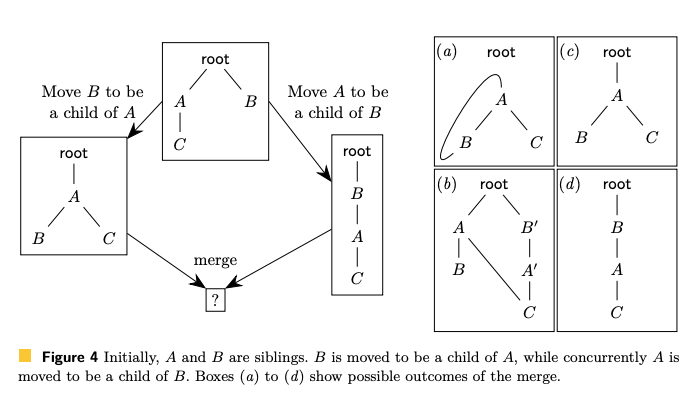
그림 4에 좀 더 미묘한 충돌을 표현는데, B를 A의 하위 항목으로 이동하고 동시에 A를 B의 하위 항목으로 이동한다. CRDT가 이 상황을 감지하지 못하면 그림 4 (a)와 같이 병합 결과처럼 상호 참조가 발생한다. 이 결과는 더 이상 트리가 아니다. 그러한 충돌하는 Move Operation을 다루는 것은 어려운 문제이며, 트리 CRDT의 기존 구현들은 이 문제에 대한 적절한 해결책을 찾지 못했다.

XML과 JSON 데이터에 대한 여러 CRDT 트리 데이터타입이 제안되었지만, 누구도 Move Operation을 정의하지 않았다. Tao et al.은 충돌하는 브랜치 노드(디렉토리)가 복제되고 리프 노드(파일)가 여러 브랜치 노드에서 참조 될 수 있는 CRDT 기반의 복제 된 파일 시스템을 구현하여 그림 4(b)와 같은 동시 동작을 해결했다. 따라서 엄격하게는 Tao 데이터 구조는 DAG(Directed acyclic graph)이며 트리가 아니다.

Najafzadeh는 또한 CRDT 기반의 복제 된 파일 시스템을 구현했지만 다른 접근 방법을 선택했다. Move Operation은 시작 전에 전역 잠금(Lock)을 획득해야 하며 충돌하는 동시 Move Operation이 처음에는 발생할 수 없도록 보장해야한다. 이러한 보수적 인 접근 방식은 Move 충돌을 배제하지만, 일부 Operation의 경우 매우 일관된 동기화가 필요하기 때문에 엄밀하게는 CRDT가 아니다.

5.2 원자 이동 가능한 트리(Tree with Atomic Moves)

이제 자유롭게 원자 이동이 가능한 트리 CRDT를 정의하고 OpSets 접근 방식의 장점에 대해 알아보자. 이 트리는 그림 4의 a, b 상황과 같은 트리 구조에 위반 없고 동시 이동으로 트리가 복제되는 일이 발생하지 않는다. 또한 잠금 장치(Lock) 이나 전역 동기화가 필요없다.

OpSet에서 충돌하는 Move Operation이 발생하면, 그 중 하나를 선택하고 적용한 뒤 다른 작업은 무시한다. 따라서 그림 4에서, 두 개의 상반되는 이동 동작의 병합 된 결과는 (c) 또는 (d) 중 하나이다. 두 사용자가 동일한 항목을 다른 위치로 동시에 이동하면 큰 ID로 Move Operation이 항목의 최종 위치를 결정한다. 그러나 비 충돌 상황에서는 모든 동시 Move Operation이 적용된다.

트리를 3장에 명시된 제한된 형태의 객체 그래프를 정의한다. 먼저 지정된 루트 객체가 필요한데, 다른 모든 Operation ID보다 (2.1절에서 소개한 전체 식별자 순서 중) 작은 Operation ID의 루트가 있다고 가정한다. 그리고 임의의 OpSet O를 트리로 정의한다면 루트 노드가 리스트나 맵인지에 따라 (root, MakeList) ∈ O 또는 (root, MakeMap) ∈ O를 만족한다. x의 값 중 하나가 y를 참조할 경우, 객체 x를 객체 y의 부모로 정의한다. 조상(ancestor) 관계는 요소 관계 E를 사용하여 정의한 부모 관계의 이행적 폐쇄(Transitive Closure)이다.

루트가 Parent가 없고 모든 루트가 아닌 노드가 하나의 Parent를 가지며 조상 관계에 사이클이없는 경우 객체 그래프는 트리이다. 이 트리 불변조건(invariant)을 만족하기 위해서 3.2절의 Operation 해석을 재정의한다. 실제로, Assign의 해석만 재정의하고 나머지 다섯 가지 Operation의 해석은 변경하지 않아도 된다.

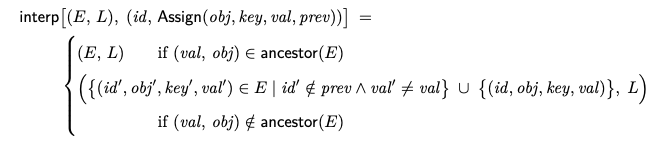
이 정의는 3.2절과 두 가지 차이점이 있다. 첫째, val이 부모 obj의 조상인 경우, Operation이 적용되지 않는데, 해당 Operation로 Tree에 순환 참조가 발생하기 때문이다. 둘째, 동일한 값 val을 참조하는 E의 기존 튜플이 제거되어 모든 루트가 아닌 노드가 정확히 하나의 부모를 가져야한다는 불변조건이 유지된다. 이 Assign Operation의 해석은 val이 트리의 기존 객체의 ID 일 때, 원자 이동을 수행하는데, 기존의 위치로부터 obj 내의 key를 변경한다. val이 기존 트리에 존재하지 않으면(방금 생성된 경우), Operation은 일반적인 Assign과 동일하게 동작한다.

6. 관련 작업

6.1 Operation의 순차적 해석

Operation의 전체 순서를 정하고 이를 순서대로 실행한다는 일반적 방식은 여러 컴퓨팅 영역에서 활용되었다. 예를 들어, 복제에 대한 상태 머신 접근법(state machine approach to replication), 데이터 모델링에 대한 이벤트 소싱 접근법(event sourcing approach to data modelling), 크래시 복구를 위한 로그 미리 쓰기(write-ahead logs for crash recovery), 직렬화 트랜잭션(serializable transaction) 그리고 확장 가능한 멀티 코어 데이터 구조(scalable multi core data structures)가 있다. OpSet 시스템은 (데이터가 복제되고 분산 되어 있다는) 피상적 유사성이 있지만 중요한 차이점을 갖고 있다.

2.3절에서 알아본 것처럼, 많은 시스템은 특정 Operation이 실행 된 후 모든 후속 Operation이 전체 순서(total order)를 보장하며 실행되어야 한다는 제약에 의존한다. 즉, Operation 시퀀스는 append-only 로그이므로 새 Operation을 기존 Operation보다 먼저 삽입 할 필요가 없었다. 이것은 분산 시스템에서 분산 된 컨센서스(consensus)를 해결하는 것과 같은 원자적 브로드캐스트(혹은 total order 브로드캐스트) 프로토콜을 필요로 한다. 이런 유형의 프로토콜은 진행을 위해서 노드들의 쿼럼과 통신이 필요하고 완전한 비동기 상태에서는 진행할 수 없다.

대조적으로, 2.2절의 순차 OpSet 해석은 임의의 순서로 OpSet에 Operation을 추가 할 수 있고 조정(coordination)없이 Operation ID를 할당하므로 원자적 브로드캐스트가 필요 없다. 이 방식의 시스템은 흔하지 않다. 가장 밀접하게 관련된 이전 연구는 타임 스탬프 순서에서 결정적으로 임시 트랜잭션을 실행한 Bayou system과 Burckhardt의 표준 충돌 해결 방법이다. OpSet 접근방식과 유사한 이 시스템들은 작은 ID로 새로운 Operation을 수신 할 때, 더 큰 ID를 가진 Operation의 실행 취소하고 다시 적용한다.

이 논문의 기여(contribution)는 OpSet 접근 방식을 이용해서 리스트와 트리 같이 복잡한 복제 된 데이터 구조를 정의, 추론하고 이전 보다 일반적으로 공식화하는 것이다. RGA가 OpSet 기반 스펙을 충족하고 그림 2에서 설명한 인터리빙 예외가 없음을 증명했다.

Baquero et a과 Grishchenko는 Operation 간의 인과 관계를 포착하기 위해 Operation의 부분 순서 로그를 CRDT로 표현할 것을 제안했다. OpSet 접근 방식은 식별자에 대한 전체 순서(total order)를 부분 순서(partial order)의 선형 확장으로 정의하는 변형으로 볼 수 있다.

6.2 복제 데이터타입의 정의와 검증

공유 데이터 구조를 공동 편집하는 알고리즘은 Operational Transformation, CRDT에서 약 30 년간 활발히 연구 되었지만 알고리즘의 정확한 일관성(exact consistency property)이 다소 불명확 했다. 예를 들어, Sun et al은 표현한 세 가지 바람직한 성질, 즉 수렴(convergence), 인과 관계 보전(causality preservation), 의도 보존(intention preservation)을 비공식적 표현했다. 처음 두 속성의 정의가 명확하지는 않지만 “의도 보존”의 정의는 더 많은 해석의 여지가 있었다.

(생략…)

6.3 협업 가능한 트리 데이터타입

그 동안 트리 데이터 구조의 공동 편집을 위해서 여러 CRDT와 OT 알고리즘이 제안되었지만 대부분의 경우 노드의 삽입, 삭제만 고려하고 이동 Operation은 지원하지 않았다.

5장에서 설명한 것처럼 트리에서 새 위치로 특정 트리를 이동하는 Operation을 지원하면 추가로 처리해야 할 충돌이 발생한다. Ahmed Nacer et al은 구체적인 알고리즘을 제시하지 않았고 이러한 충돌을 처리하는 방법을 조사했다. Tao et al은 이동 Operation 처리중 충돌 발생시 동일한 객체가 둘 이상의 위치에 나타날 수 있도록할 것을 제안했는데, 이는 엄격하게는 DAG이며 트리가 아니다.

Najafzadeh는 이동 Operation의 전제 조건이 안정적이지 않기 때문에 동시 이동 Operation을 CRDT로 안전하게 구현할 수 없다고 주장했다. Najafzadeh는 잠금장치를 사용하여 전역으로 이동 Operation을 동기화하여 그림 4와 같은 예외를 처리했지만 일부 Operation이 strong consistency 동기화가 필요하기 때문에 해당 데이터타입은 CRDT가 아니다.

5장에 명시한 이동은 완전 비동기 트리 CRDT의 첫 번째 정의이고 Najafzadeh가 주장한 명백한 모순을 회피했다. Operation을 생성하는 시점에 전제 조건 (val, obj) !∈ ancestor(E)를 평가하는 대신에 결정적 순서로 모든 Operation을 적용한다.

7. 결론

이 논문은 복제 된 데이터타입의 의미론을 명시하기 위한 간단하지만 강력한 Operation Sets(OpSets)를 제안했다. OpSets 모델에서 다양하고 공통적으로 복제 가능한 데이터타입을 명시하고 Isabelle/HOL을 사용하여 형식적으로 그 속성을 추론했다. OpSets를 사용하여 기존 협업 텍스트 편집 알고리즘에서 발생하는 인터리빙 예외를 확인했고 RGA 알고리즘이 OpSets 리스트 스펙을 충족 시키는 것을 입증했다. 마지막으로 OpSet 모델을 사용하여 새로운 복제 알고리즘을 개발하는 방법에 대해 알아봤고 트리 CRDT에서 원자적 이동 Operation에 대한 스펙을 제안했다.

OpSets는 일부 업데이트들이 적용된 후 복제본의 허용 상태를 정확하게 정의한 실행 가능한 스펙이다. 이 문서에서는 순차적인 OpSet 해석을 사용했다. Operation은 ID의 엄격한 오름차순으로 적용되는 이는 수렴(convergence)을 쉽게 보장하고 CRDT의 스펙, 불변조건에 대한 추론을 단순화하므로 매우 유용하다. 이와 반대로 이전 CRDT를 정의한 전통적인 접근법은 Operation이 교환법칙(commutative)을 만족해야했고 복잡성 높았다. RGA가 OpSets 리스트 스펙을 만족함을 증명할 때, 순차적 명세와 교환 적 구현 사이의 일치성을 입증했다. 이는 향후 작업을 위해서 다른 데이터타입에 대한 이 가설을 더 자세히 살펴 볼때 유용할 것이다. 특히, 5장에서는 분산 P2P 파일 시스템을 구현할 수 있으며 교환법칙을 만족한 이동 Operation을 갖는 트리 CRDT를 제안했다.

이 논문에서는 순차적인 OpSet 해석에 초점을 맞추었지만, 특정 결정적(deterministic) 함수를 해석 함수 [-]로 사용될 수 있다는 점을 주목하자. 특히 해석 함수를 데이터베이스의 쿼리로 생각해본다면 OpSet을 공유 데이터에 대한 모든 변경 사항을 처리하는 데이터베이스로 볼 수 있다. 결과로 생성 된 데이터타입은 데이터베이스의 materialized view에 해당된다. OpSet O에 새로운 Operation이 추가되면 [O]에 해당하는 변화를 계산하는 것은 최적화 된 알고리즘이 개발 된 materialized view의 관리 문제이다. 이러한 기술을 복제 된 데이터타입에 적용 할 수 있으며 효율적인 CRDT 구현을 OpSet 기반 스펙에서 파생시킬 수 있다고 생각한다.

(Appendix 생략…)

원본 논문 링크

• OpSets: Sequential Specifications for Replicated Datatypes (Extended Version).